博弈题骗分失败,然后168分(
你们这是什么比赛啊,你们这比赛……你们这比赛 你们这比赛nb(x
A 核酸检测
题目:
新型冠状病毒疫情爆发!某城市内大量疑似患者被集中到各个隔离点,初期确诊非常困难,专家团队需要依次到这些隔离点去现场指导,为疑似患者进行核酸检测。
城市共有n*(n+1)个隔离点,它们形成了n行n+1列的方阵。我们用(r,c)表示位于从上到下第r行、从左到右第c列的隔离点。例如,左上角的坐标是(1,1),右下角的坐标是(n,n+1)。
该城市的交通结构比较特殊,任意两个对角方向的相邻隔离点之间有一条双向通路。此外,在方阵的边界处有一条顺时针运行的单向地铁环线。下图是一个n=5的城市示意图:
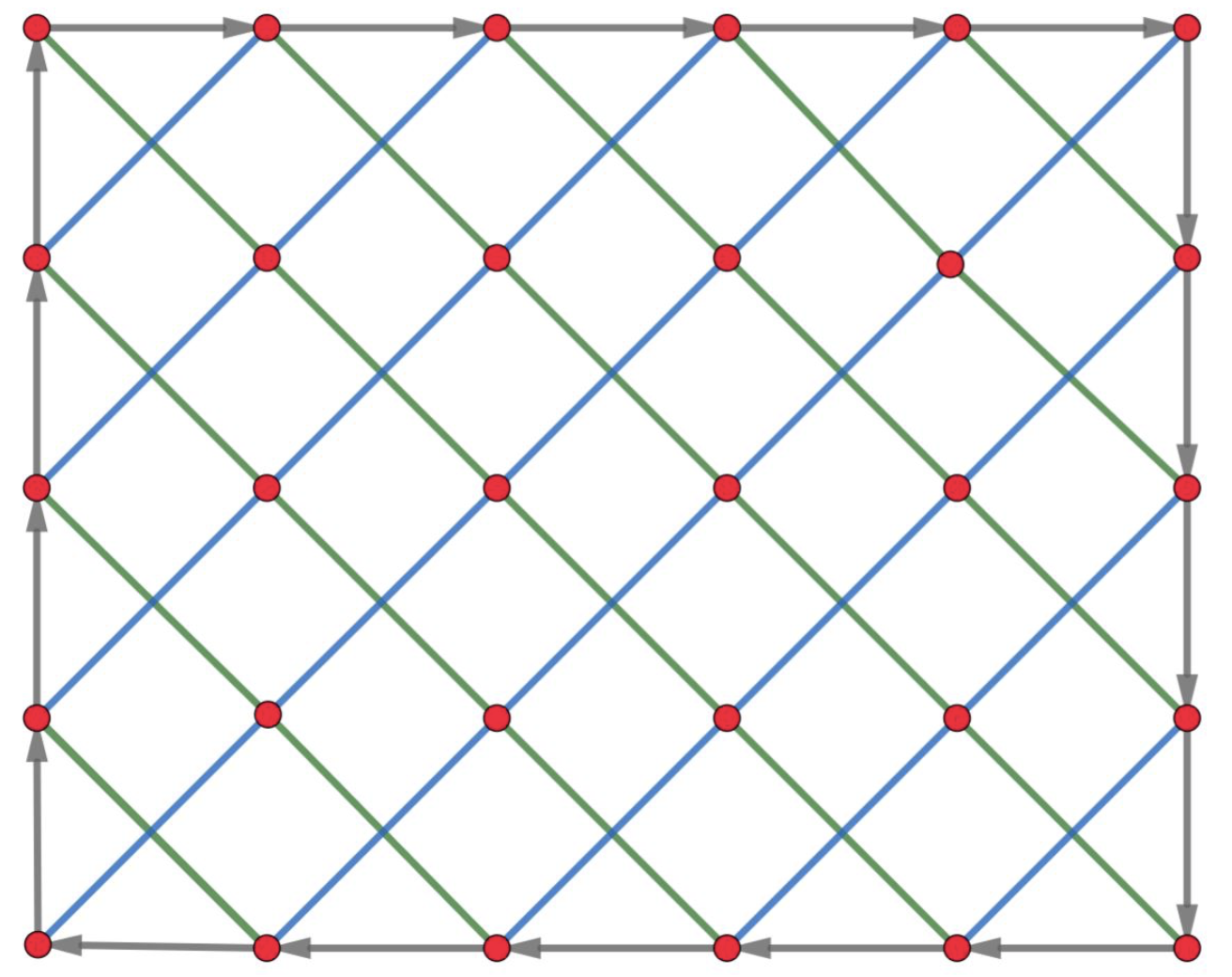
专家可以从任意一个隔离点出发,之后你可以沿着道路或乘坐地铁前往其他隔离点。走过一条道路、乘坐一段地铁都需要1单位时间。在隔离点处进行核酸检测所需的时间忽略不计。
专家迫切想要知道最少需要多少时间才能完成所有隔离点的核酸检测。请求出最少需要的时间,以及一条路线。
即,n*(n+1)的点阵图,已知内部对角线可任意走,外部有顺时针的可行路线,求最短的能够经过所有点的路径长度(通过画图可以证明一定存在哈密顿通路且该即为答案),并输出该通路。
其实画图画着画着就有了也不难,就是得多画画图,其中我在比赛时的解法如下:
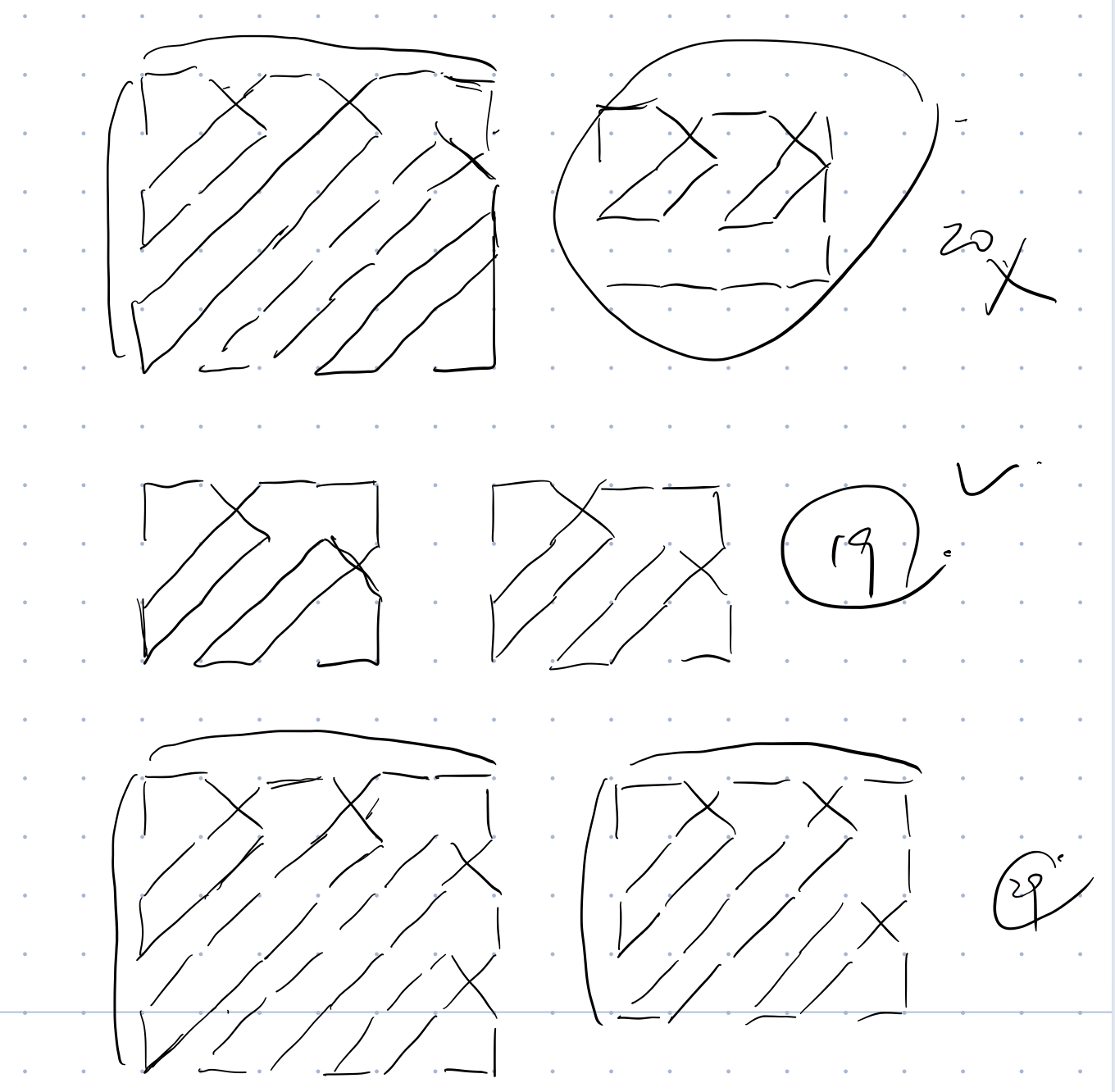
另外,标称也给出了一种更简单的画法,具体可见参考代码。
B 齐心抗疫
题目:
某市有n个县,并有n-1条双向高速公路连通这n个县,每条高速公路的长度为1。
受疫情影响,第i个县里有a[i]个患者。为了让疫情较轻的县帮助疫情严重的县,政府决定选择两个县 ,x的疫情较为不严重,y的疫情较为严重(即a[x]<=a[y]),并让县 x帮助县y。县 x将为县 y的每一个患者送一份医疗物资,以最短路从x到y运输,运送一份医疗物资通过长度为1的高速公路需要花费1元,由政府掏钱报销。
请问如果任意选择两个县实施帮扶计划,政府最多要花多少钱?
假的最短路问题。对于前两个测试点确实可以用Floyd算法()实际上稍微注意一下只有n-1条边就可以知道这个结构更精确的讲是一棵树。
另外,对于\(ans(i,j)=dis(i,j)*max(a[i],a[j])=max(dis(i,j)*a[i],dis(i,j)*a[j])\)故对于每个结点,只需要求出距离其最远的结点,并乘上自己的a[i],即为该节点能提供的最大贡献值。
对于求结点到树上结点的最大距离,有结点到树直径的其中一端的距离最大。求树的直径可先对任意x,求出树上距离其最远的点y,再由y求距离其最远的z,则y和z即为树直径的两端。
#include<cstdio>
#include<vector>
#include<cmath>
#define pb push_back
int n;
int a[50010];
vector<int>G[50010];
int dx[50010],dy[50010];
int dfs(int now,int pre,int* d){
int res=now;
for(int i=0;i<G[now].size();i++){
int nxt=G[now][i];
if(nxt==pre)continue;
d[nxt]=d[now]+1;
int tmp=dfs(nxt,now,d);
if(d[tmp]>d[res]) res=tmp;
}
return res;
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
int tx,ty;
for(int i=1;i<=n-1;i++){
scanf("%d%d",&tx,&ty);
G[tx].pb(ty);G[ty].pb(tx);
}
int x=dfs(1,0,dy);
int y=dfs(x,0,dx);
fill(dy,dy+50010,0);dfs(y,0,dy);
int ans=-1;
for(int i=1;i<=n;i++){
ans=max(ans,a[i]*max(dx[i],dy[i]));
}
printf("%d\n",ans);
}
D 抗议斗争
题目:
新冠疫情爆发以来,病毒不断地扩散传播,而人类也在不断采取各种措施遏制病毒传播。于是我们可以为这场抗疫斗争建立一个数学模型,将病毒的不断传播和人类的不断采取措施抽象为一场双方轮流行动的博弈。我们认为人类与病毒的每轮行动都可以选择一个正整数作为行动值来评估。然而,出于各方面限制,双方的所有行动值总和必须等于一个数m,且每次的行动值不能超过对方上轮的行动值。对人类来说,要遏制疫情,就应成为最后行动的一方,也就是说,在本方的某次行动后,行动值总和m恰好被消耗完。
假设人类先行动,那么我们只需一鼓作气消耗完所有m点行动值,就能战胜病毒。然而在最开始的阶段出于认识不到疫情的严重性,往往最难开展大规模行动。出于这个原因,我们令h[m]表示在行动值总和为m的情况下,人类(即先行动方)的第一次行动最少要多少行动值,才能保证自己必胜。
出于统计需要,某科学家记 \(f_i=\sum_{m|i}h_m\) ,并想知道 \(\sum_{i=1}^nf_i\) 。方便起见,对998244353取模。你能帮个忙吗?
(比赛的时候果然题目读错了(x
①能够通过1e5复杂度的部分:首先是对于h[m]的部分,易得若m为奇数,则h[m]必为1,因为此时在后序回合中双方均只能每次消耗1,且人类方能够先用完;若m为偶数,则h[m]必为偶数,若为奇数则当到病毒回合时会剩余奇数,则对于病毒而言会到达必胜点(病毒只需此时消耗1即可胜利),且由于每一步最优,有 \(h_{2m}=2h_m\ \ \ \ \\) 即可得到\(h_m=lowbit(m)\)。
故只需要O(n)预处理一下h[1……n]即可。
———以下是待update的部分qwq———
②能通过1e11的部分:分块处理,让复杂度达到O(√n)

